Menghitung Ukuran Pemusatan: Mean, Median, Modus dan contoh - Selamat sore teman Sains Seru, sekarang kita akan membahas tentang Ukuran Pemusatan: Mean, Median, Modus. Dalam materi Statistik ini kita akan membahas seputaran mean, median, dan modus yang sering keluar dalam kehidupan. Baik kita akan langsung membahasnya dibawah, maka simak baik-baik ya.
Ukuran pemusatan data merupakan suatu nilai yang ada di dalam kumpulan data yang dimana dapat mewakili kumpulan data tersebut. Suatu rangkaian data biasanya mempunyai kecenderungan untuk terkonsentrasi atau terpusat pada nilai pemusatan ini. Ukuran pemusatan adalah ukuran statistik yang dapat menjadi pusat dari rangkaian pusat dari rangkaian data dan memberi gambaran singkat tentang data.
Dari kumpulan data mentah diatas, kita belum bisa menyimpulkan tentang nilai data itu. Terdapat tiga nilai statistik yang dapat dipakai untuk menjelaskan kumpulan data diatas, yaitu rataan (mean), median, dan modus. Untuk lebih jelasnya kita simak penjelasan dibawah.
Keterangan: ∑x (dibaca : sigma) = jumlah data
n = banyaknya data
xi = data ke-i
Contoh 1.
Dari hasil tes 10 siswa kelas XI diperoleh data: 3, 7, 6, 5, 3, 6, 9, 8, 7, dan 6. Tentukan rataan atau mean dari data tersebut.
Jadi, rataannya atau mean adalah 6,0.
Keterangan: fi = frekuensi untuk nilai xi
xi = data ke-i
Contoh 2.
Data hasil ulangan harian mtk di kelas XI program IPA, dimana terdapat enam siswa mendapat nilai 8, tujuh siswa mendapat nilai 7, lima siswa mendapat nilai 6, tujuh siswa mendapat nilai 5, dan lima siswa mendapat nilai 4. Tentukan rata-rata atau mean nilai ulangan harian Matematika dikelas tersebut.
Jadi, rata-rata atau mean nilai ulangan Matematika di kelas XI IPA adalah 6,05.
Contoh 3.
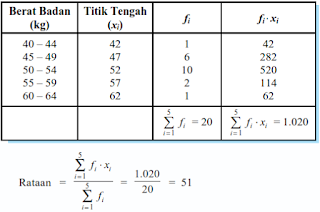
Tentukan rata-rata atau mean dari data berikut.
Jadi, rata-rata atau meannya adalah 51.
Selain dengan cara diatas, ada cara lain untuk menghitung rata-rata atau mean yaitu dengan menentukan mean sementara terlebih dahulu sebagai berikut.
(a) Menentukan rata-rata atau mean sementara.
(b) Menentukan simpangan (d) dari rata-rata atau mean sementara.
(c) Menghitung simpangan rata-rata atau mean baru dengan rumus berikut ini.
(d) Menghitung rata-rata atau mean sesungguhnya.
Keterangan: xs = rata-rata sementara
∑fi.di = jumlah frekuensi × simpangan
Contoh 4.
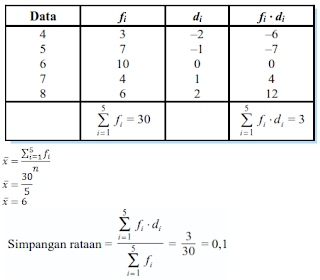
Carilah rata-rata dari data berikut dengan menggunakan rataan sementara.
Rata-rata = rata-rata sementara + simpangan rata-rata
= 6 + 0,1
= 6,1
Contoh 5.
Dari data dibawah ini, tentukan nilai mediannya.
Jadi, mediannya adalah 6.
2. Banyaknya data n = 50 (genap), maka menggunkaan rumus:
Keterangan: b₂ = tepi bawah kelas median
c = lebar kelas
N = banyak data
F = frekuensi kumulatif kurang dari sebelum kelas median
f = frekuensi kelas median
Contoh 6.
Tentukan median dari data tes Matematia terhadap 40 siswa kelas XI IPA yang digambarkan pada tabel distribusi frekuensi dibawah ini.
Contoh 7.
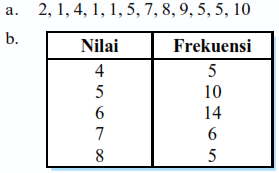
Tentukan modus dari data dibawah ini.
Data yang sering muncul adalah 1 dan 5. Jadi modusnya adalah 1 dan 5 (bimodal).
b. Berdasarkan data dari tabel, nilai yang memiliki frekuensi tertinggi adalah 6 dengan frekusni 14. Jadi modusnya adalah 6.
Keterangan: b₀ = tepi bawah kelas modus
l = lebar kelas
d₁ = selisih frekuensi kelas modus dengan kelas sebelumnya
d₂ = selisih frekuensi kelas modus dengan kelas sesudahnya
Contoh 8.
Tentukan modus dari tabel dibawah ini.
Menghitung Ukuran Pemusatan: Mean, Median, Modus dan contoh - Mungkin sekian dulu ya pembahasan tentang Ukuran Pemusatan: Mean, Median, Modus. Semoga pembahasan diatas dapat bermanfaat bagi teman setia Sains Seru. Jika ada yang mau ditanyakan bisa tinggalkan di kolom komentar dibawah ya. Untuk pembahasan Ukuran Pemusatan dan Ukuran Penyebaran Data dapat ikuti terus update artikel disini ya. Terimakasih atas perhatiannya, See You.
Ukuran Pemusatan
Misalkan diberikan data umur dari 10 siswa calon paskibraka
18 16 15 15 17
16 16 17 18 18
1. Rataan (mean)
Nilai rataan (mean) adalah salah satu ukuran yang memberikan gambaran yang lebih jelas dan singkat tentang sekelompok data mengenai suatu masalah, baik tentang sampel atau populasi. Rata-rata atau mean yang didapat dari hasil pengukuran sampel disebut statistik, sedangkan Rata-rata atau mean yang didapat dari data populasi disebut parameter. Rataan atau mean biasa di simbolkan dengan ẋ (dibaca : x bar atau x rata-rata). Dibawah ini kita akan membahas cara menghitung mean.a. Mean Data Tunggal
Mean data tunggal adalah jumlah data dibagi dengan banyaknya data. Secara matematis dinyatakan sebagai berikut.Keterangan: ∑x (dibaca : sigma) = jumlah data
n = banyaknya data
xi = data ke-i
Contoh 1.
Dari hasil tes 10 siswa kelas XI diperoleh data: 3, 7, 6, 5, 3, 6, 9, 8, 7, dan 6. Tentukan rataan atau mean dari data tersebut.
Jawab
Jadi, rataannya atau mean adalah 6,0.
b. Mean dari Data Distribusi Frekuensi
Apabila data yang diberikan dalam bentuk tabel distribusi frekuensi maka mean dapat diselesaikan dengan rumus sebagai berikut.Keterangan: fi = frekuensi untuk nilai xi
xi = data ke-i
Contoh 2.
Data hasil ulangan harian mtk di kelas XI program IPA, dimana terdapat enam siswa mendapat nilai 8, tujuh siswa mendapat nilai 7, lima siswa mendapat nilai 6, tujuh siswa mendapat nilai 5, dan lima siswa mendapat nilai 4. Tentukan rata-rata atau mean nilai ulangan harian Matematika dikelas tersebut.
Jawab
Data diatas dapat disajikan dalam tabel seperti dibawah ini.Jadi, rata-rata atau mean nilai ulangan Matematika di kelas XI IPA adalah 6,05.
c. Mean Data Bergolong
Apabila data yang diberikan dalam bentuk data bergolong hakikatnya sama dengan menghitung mean data pada distribusi frekuensi tunggal dengan mengambil tiik tengah kelas sebagai xi.Contoh 3.
Tentukan rata-rata atau mean dari data berikut.
Jawab
Jadi, rata-rata atau meannya adalah 51.
Selain dengan cara diatas, ada cara lain untuk menghitung rata-rata atau mean yaitu dengan menentukan mean sementara terlebih dahulu sebagai berikut.
(a) Menentukan rata-rata atau mean sementara.
(b) Menentukan simpangan (d) dari rata-rata atau mean sementara.
(c) Menghitung simpangan rata-rata atau mean baru dengan rumus berikut ini.
(d) Menghitung rata-rata atau mean sesungguhnya.
Keterangan: xs = rata-rata sementara
∑fi.di = jumlah frekuensi × simpangan
Contoh 4.
Carilah rata-rata dari data berikut dengan menggunakan rataan sementara.
Jawab
Rata-rata = rata-rata sementara + simpangan rata-rata
= 6 + 0,1
= 6,1
2. Median
Median adalah data yang terletak di tengah setelah data tersebut disusun menurut urutan nilainya. Median dilambangkan dengan Me. Nilai Me sering dipakai untuk menjelaskan kecenderungan pemusatan data apabila pada data tersebut ditemukan nilai-nilai yang ekstrim, sehingga tidak cukup dijelaskan melalui nilai rata-rata saja.a. Median data tunggal
Median data tunggal dapat dihitung menggunakan rumus sebagai berikut.Contoh 5.
Dari data dibawah ini, tentukan nilai mediannya.
Jawab
1. Data diurutkan menjadi:Jadi, mediannya adalah 6.
2. Banyaknya data n = 50 (genap), maka menggunkaan rumus:
b. Median data bergolong
Jika data disajikan dengan data bergolong, artinya data itu dikelompokkan dalam interval-interval kelas yang sama. Rumus yang digunakan adalah sebgai berikut.Keterangan: b₂ = tepi bawah kelas median
c = lebar kelas
N = banyak data
F = frekuensi kumulatif kurang dari sebelum kelas median
f = frekuensi kelas median
Contoh 6.
Tentukan median dari data tes Matematia terhadap 40 siswa kelas XI IPA yang digambarkan pada tabel distribusi frekuensi dibawah ini.
Jawab
3. Modus
Modus adalah nilai yang paling sering muncul atau nilai yang mempunyai frekuensi tertinggi. Jika suatu data hanya mempunyai satu modus disebut unimodal, dan bila memiliki dua modus disebut bimodal, sedangkan jika memiliki modus lebih dari dua disebut multimodal. Modus dilambangkan dengan Mo.a. Modus data tunggal
Modus data tunggal adalah data yang sering muncul atau data dengan frekuensi tinggi.Contoh 7.
Tentukan modus dari data dibawah ini.
Jawab
a. 1, 1, 1, 2, 4, 5, 5, 5, 7, 8, 9, 10Data yang sering muncul adalah 1 dan 5. Jadi modusnya adalah 1 dan 5 (bimodal).
b. Berdasarkan data dari tabel, nilai yang memiliki frekuensi tertinggi adalah 6 dengan frekusni 14. Jadi modusnya adalah 6.
b. Modus data bergolong
Modus data bergolong dirumuskan sebagai berikut.Keterangan: b₀ = tepi bawah kelas modus
l = lebar kelas
d₁ = selisih frekuensi kelas modus dengan kelas sebelumnya
d₂ = selisih frekuensi kelas modus dengan kelas sesudahnya
Contoh 8.
Tentukan modus dari tabel dibawah ini.
Jawab
Frekuensi tertinggi 18, kelas 65 - 69.Menghitung Ukuran Pemusatan: Mean, Median, Modus dan contoh - Mungkin sekian dulu ya pembahasan tentang Ukuran Pemusatan: Mean, Median, Modus. Semoga pembahasan diatas dapat bermanfaat bagi teman setia Sains Seru. Jika ada yang mau ditanyakan bisa tinggalkan di kolom komentar dibawah ya. Untuk pembahasan Ukuran Pemusatan dan Ukuran Penyebaran Data dapat ikuti terus update artikel disini ya. Terimakasih atas perhatiannya, See You.