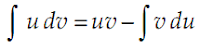Rumus Lengkap Integral Tak Tentu: Contoh dan Pembahasannya - Selamat sore teman Sains Seru, kali ini kita akan membahas tentang Integral Tak Tentu. Materi ini ada di kelas XII SMA yang biasanya sering keluar soalnya di Ujian Nasional (UN) SMA. Bukan hanya itu materi ini juga sering keluar di tes masuk perguruan tinggi SBMPTN. Maka dari itu dimohonkan teman Sains Seru menyimak pembahasan dibawah ini.
 |
| Google Image - Rumus Lengkap Integral Tak Tentu: Contoh dan Pembahasannya |
Bagaimana kalau sekarang kita balik fungsi f '(x) maka antiturunannya adalah f(x) atau jika diurai, tampak bahwa jika f '(x) = xⁿ maka f(x) = 1 / (n + 1) xⁿ⁺¹ + c.
Integral Tak Tentu
Integral tak tentu adalah integral yang belum memiliki batas bawah dan batas atas. Di bagian diatas telah dijelaskan bahwa integral merupakan antiturunan. Jadi, apabila terdapat fungsi F(x) yang bisa di diferensial pada interval [a, b] sehingga d(F(x)) / dx = f(x). Secara matematis bisa ditulis sebagai berikut.
∫ f(x) dx = F(x) + c
Keterangan: ∫ dx = lambang integral (antiturunan).
f(x) = fungsi integran, yaitu fungsi yang dicari antiturunannya.
c = konstanta.
Persamaan diatas merupakan persamaan integral secara umum yang dimana integral (satu antiturunan untuk setiap nilai konstanta c). Persamaan diatas digunakan untuk membuktikan teorema-teorema berikut yang akan membantu teman Sains Seru mengerjakan perhitungan integral.
Disini kita akan akan memberikan 7 teorema yang bisa teman Sains Seru gunakan untuk menghitung soal dari integral. Ketujuh teorema integral tak tentu dapat dilihat seperti gambar dibawah ini.
a. Teorema 1.
Jika n bilangan rasional dan n tidak sama dengan 0, maka
Pembuktian.
Untuk dapat membuktikan Teorema 1, teman Sains Seru bisa mendiferensialkan xⁿ⁺¹ + c yang terdapat pada ruas kanan seperti berikut.
b. Teorema 2.
Jika f fungsi yang terintegralkan dan k suatu konstanta, maka
c. Teorema 3.
Jika f dan g fungsi-fungsi yang terintegralkan, maka
d. Teorema 4.
Jika f dan g fungsi-fungsi yang terintegralkan, maka
Pembuktian.
Untuk dapat membuktikan teorema 4, teman Sains Seru dapat mendiferensialkan ∫ f(x) dx ± ∫ g(x) dx yang terdapat pada ruas kanan sebagai berikut.
Contoh 1.
Hitunglah integral dari ∫ (3x² - 3x + 7) dx!
Jawab
e. Teorema 5.
Aturan integral subtitusi
Jika u suatu fungsi yang dapat di diferensialkan dan r suatu bilangan rasional tak 0 (nol), maka
di mana c adalah konstanta dan r tidak sama dengan -1
f. Teorema 6.
Aturan integral parsial
Jika u dan v fungsi-fungsi yang dapat di diferensialkan, maka
Pembuktian.
Pada pembahasan artikel sebelumnya turunan, teman Sains Seru telah mengetahui turunan hasil kali dua fungsi ∫ f(x) = u(x) . v(x) adalah d/dx [u(x)v(x)] = u(x) . v'(x) + v(x) . u'(x). Akan dibuktikan aturan integral parsial dengan rumus tersebut. Caranya adalah dengan mengintegralkan kedua persamaan seperti berikut.
g. Teorema 7.
Aturan integral trigonometri
di mana c adalah konstanta.
Pembuktian.
Pada pembahasan artikel sebelumnya turunan, teman Sains Seru telah mengetahui turunan fungsi trigonometri, yaitu d/dx (sin x) = cos x, d/dx (cos x) = -sin x, dan d/dx (tan x) = sec² x.
Berikut ini akan dibuktikan aturan integral trigonometri menggunakan rumus tersebut. Cara yang digunakan yaitu dengan mengintegralkan kedua ruas seperti berikut.
Aturan Integral Subtitusi
Integral subtitusi atau sama dengan yang tertulis diatas (Teorema 5). Aturan ini digunakan untuk memecahkan masalah pengintegralan yang tidak dapat diselesaikan dengan rumus-rumus dasar yang telah teman Sains Seru pelajari.Contoh 2.
Hitunglah integral dibawah ini.
Jawab
a. Misalkan u = 9 - x², maka du = -2x dxx dx = du/-2
b. Misalkan u = √x = x½
c. Misalkan u = 1 - 2x², maka du = -4x dx
dx = du/-4x
sehingga integral tersebut dapat ditulis sebagai berikut.
Integral dengan Bentuk √a² - x² , √a² + x² , √x² - a²
Integral dalam bentuk √a² - x² , √a² + x² , √x² - a² dapat diselesaikan dengan menggunakan metode subtitusi x = a sin t, x = a tan t, dan x = a sec t. Sehingga nantinya akan diperoleh seperti berikut.Tambahan juga integral trigonometri.
Contoh 3.
Hitunglah setiap integral berikut!
Jawab
a. Untuk mengerjakan integral ini, terlebih dahulu teman Sains Seru mengubah sin(3x + 1) cos(3x + 1) ke dalam rumus trigonometri sudut rangkap, yaitub. Misalkan x = 3 sin t, maka sin t = x/3
dx = 3 cos t dt.
Sekarang perhatikan gambar segitiga dibawah ini.
Contoh 4.
Jika g'(x) = 2x - 3 dan g(2) = 1, tentukanlah persamaan g(x).
Jawab
Contoh 5.
Terdapat sebuah melalui titik (-2, 12) yang memiliki gradien garis singgung dy/dx = 6x - 15. Tentukan persamaan kurva yang terbentuk.
Jawab
Jadi, persamaan kurva tersebut adalah f(x) = 3x² - 15x - 30.Rumus Lengkap Integral Tak Tentu: Contoh dan Pembahasannya - Mungkin sampai disini dulu ya pembahasan tentang Integral Tak Tentu. Semoga pembahasan singkat diatas dapat bermanfaat bagi teman setia Sains Seru. Jika ada yang mau ditanyakan bisa tinggalkan di kolom komentar dibawah ya. Untuk pembahasan Integral Tertentu dan Aplikasi dari Integral (Luas dan Volume) dapat ikuti terus update artikel disini ya. Terimakasih atas perhatiannya, See You.