Contoh Soal dan Pembahasan Trigonometri Lengkap Kelas 11 - Di kesempatan kali ini kita akan memberikan Contoh Soal dan Pembahasan Trigonometri Kelas 11. Sebelumnya kita sudah pernah membahas materi tentang trigonometri jumlah dan selisih dua sudut. Untuk lebih memahaminya lagi mari kita mulai berlatih dengan soal-soal yang sudah disediakan di buku matematika kalian masing-masing. Sesuai dengan artikel sebelumnya kita akan lebih membahas soal-soal latihan agar rumus yang awalnya banyak bisa menjadi hafal dengan sendirinya jika kita sering berlatih soal-soal.
Soal yang di tuliskan disini kita ambil dari soal-soal latihan di Buku Sekolah Elektronik (BSE). Oke di ingatkan juga bagi teman Sains Seru yang ingin memberikan soalnya disini untuk dibahas bersama-sama bisa langsung kirimkan soalnya dalam bentuk tulisan atau gambar ke kolom komentar dibawah ini atau bisa langsung kirim melalui contact yang tersedia.
 |
| Google Image - Contoh Soal dan Pembahasan Trigonometri Lengkap Kelas 11 |
Soal Latihan Trigonometri Jumlah dan Selisih Dua Sudut
Baik langsung saja kita masuk ke pembahasan soal ya, jika nanti ada yang kurang jelas bisa langsung di tanyakan melalui kolom komentar dibawah. Di ingatkan kembali kalian bisa mengirimkan soal kesini untuk kita bahas bersama melalui contact atau email yang ada di website ini.
Baca juga: Materi Trigonometri Lengkap.
Soal 1.
Hitunglah nilai sudut di bawah ini tanpa menggunakan kalkulator.
a. sin 150⁰
b. sin 75⁰ cos 15⁰ - cos 75⁰ sin 15⁰
Jawab
a. Pertama-tama kita ubah terlebih dahulu nilai sudut di atas dengan sudut-sudut istimewa kemudian ubah ke dalam rumus penjumlahan sudut sin, seperti dibawah ini.
sin 150⁰ = sin (60 + 45)⁰
= sin 60⁰ cos 45⁰ + cos 60⁰ sin 45⁰
= (½√3 × ½√2) + (½ × ½√2)
= ¼√6 + ¼√2
= ¼ (√6 + √2)
Jadi, hasil dari sin 150⁰ adalah ¼ (√6 + √2).
b. sin 75⁰ cos 15⁰ - cos 75⁰ sin 15⁰ = sin (75 - 15)⁰
= sin 60⁰
= ½√3
Jadi, hasil dari sin 75⁰ cos 15⁰ - cos 75⁰ sin 15⁰ adalah ½√3.
Soal 2.
Hitunglah dengan rumus cosinus jumlah dan selisih sudut berikut.
a. cos 195⁰
b. cos 58⁰ cos 13⁰ + sin 58⁰ sin 13⁰
Jawab
a. Dengan cara yang sama kita ubah nilai diatas dan memasukan ke dalam rumus pengurangan sudut cos, seperti dibawah ini.
cos 195⁰ = cos (135 + 60)⁰
= cos 135⁰ cos 60⁰ - sin 135⁰ sin 60⁰
= (-½√2) × (½) - (½√2 × ½√3)
= (-¼√2) - (¼√6)
= -¼ (√2 + √6)
Jadi, hasil dari cos 195⁰ adalah -¼ (√2 + √6).
b. cos 58⁰ cos 13⁰ + sin 58⁰ sin 13⁰ = cos (58 - 13)⁰
= cos 45⁰
= ½√2
Jadi, hasil dari cos 58⁰ cos 13⁰ + sin 58⁰ sin 13⁰ adalah ½√2.
Soal 3.
Diketahui sin A = 3/5, cos B = 5/13, A dan B merupakan sudut lancip. Tentukan
a. tan (A + B)
b. tan (A - B)
Jawab
a. kita harus mencari nilai sin dan cos lain dengan menggunakan phytagoras dan dimana tan A = (sin A/cos A), seperti dibawah ini.
b. Dengan cara yang sama, maka
Soal 4.
Diketahui ∠A dan ∠B adalah sudut lancip, jika cos A = 4/5 dan cos B = 24/25, tentukan:
a. cos (A + B)
b. cos (A - B)
Jawab
a. Dengan cara yang sama dengan no 3 menggunakan rumus penjumlahan sudut cos, seperti dibawah ini.
b. Dengan cara yang sama dengan no 3 menggunakan rumus pengurangan sudut cos, seperti dibawah ini.
Soal 5.
Jika sin (x + 30⁰) = sin x, buktikan bahwa tan x = 2 + √3.
Jawab
Contoh Soal dan Pembahasan Trigonometri Lengkap Kelas 11 - Mungkin sampai disini dulu ya Contoh Soal dan Pembahasan Trigonometri Lengkap Kelas 11. Semoga pembahasan diatas bermanfaat bagi teman setia Sains Seru. Jika ada yang kurang jelas bisa ditanyakan dengan tinggalkan di kolom komentar dibawah ya. Untuk kesempatan selanjutnya kita akan melanjutkan pembahasan trigonometri maka dari itu ikuti terus update artikel disini ya. Terimakasih atas perhatiannya, See You.
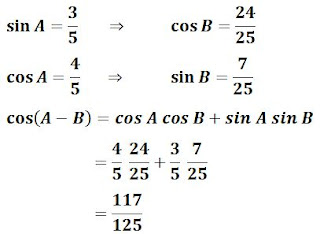
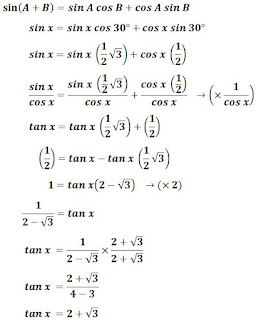
9 comments
Click here for commentsOwh tq
ReplyOwh tq
Replysalah yang soal no 3 dik sin a=3/5 tpi ppas dik 4/5 gimana sih
ReplyApanya yg lengkap?
ReplyNomor satu itu sin 150 kok jadinya sin(60+45) sih,, wkwk gimana to? :))
ReplyKo gini
Replyterimakasih sharenya.semoga menjadi pemberat amal
ReplyIn this case, the cutter can move in the Z airplane to vary levels, however not simultaneously with the X,Y movements. An exception might be that the cutter can interpolate precision machining helically, that is, do a circle in X,Y while moving simultaneously in Z to kind a helix . Imagine surfaces as the same type of spline approximation, simply multiplied many instances in the across direction with a space between .
ReplyThank yoou
Reply