Soal Latihan Fungsi Komposisi serta Pembahasannya - Oke di kesempatan kali ini kita akan melatih kemampuan pada materi kita sebelumnya yaitu Fungsi Komposisi. Pada pertemuan sebelumnya kita sudah membahas dengan lengkap materi yang berkaitan dengan Fungsi Komposisi, maka dari itu di pertemuan kali ini kita akan mengasah kemampuan kita dengan menyelesaikan soal latihan fungsi komposisi. Soal yang kita ambil di pertemuan kali ini meliputi soal latihan yan ada di buku dan Buku Sekolah Elektronik (BSE). Jadi jika nanti terdapat hal yang kurang di mengerti bisa langsung di tanyakan di kolom komentar di bagian bawah ya. Oke kita akan langsung masuk ke soal latihan fungsi komposisi beserta pembahasannya.
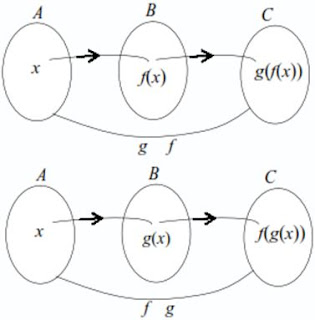 |
| Google Image - Soal Latihan Fungsi Komposisi serta Pembahasannya |
Soal Latihan Fungsi Komposisi
Bagi yang ingin bertanya soal fungsi komposisi bisa juga menuliskannya di kolom komentar, nanti akan kita diskusikan bersama.
Baca juga:
Soal Latihan Fungsi Komposisi 1.
Diketahui f(x) = x - 2 dan g(x) = x² - x - 2. Tentukanlah:
a. (f + g)(x) c. (f × g)(x)
b. (f - g)(x) d. (f / g)(x)
Jawab
a. (f + g)(x) = (x - 2) + (x² - x - 2)
= x - 2 + x² - x - 2
= x² - 4
b. (f - g)(x) = (x - 2) - (x² - x - 2)
= x - 2 - x² + x + 2
= -x² + 2x
c. (f × g)(x) = (x - 2) × (x² - x - 2)
= x³ - x² - 2x - 2x² + 2x + 4
= x³ - 3x² + 4
d. (f / g)(x) = (x - 2) / (x² - x - 2)
= (x - 2) / (x - 2)(x + 1)
= 1 / (x + 1)
Soal Latihan Fungsi Komposisi 2.
Diketahui f(x) = x² dan g(x) = x + 4. Tentukanlah:
a. (f + g)(-3) c. (f × g)(-1)
b. (f - g)(1) d. (f / g)(2)
Jawab
a. (f + g)(-3) = (x²) + (x + 4)
= (-3²) + (-3 + 4)
= 10
b. (f - g)(1) = (x²) - (x + 4)
= (1²) - (1 + 4)
= -4
c. (f × g)(-1) = (x²) × (x + 4)
= (-1²) × (-1 + 4)
= 3
d. (f / g)(2) = (x²) / (x + 4)
= (2²) / (2 + 4)
= 4 / 6
= 2 / 3
Soal Latihan Fungsi Komposisi 3.
Diketahui fungsi yang ditentukan oleh f(x) = x + 1, g(x) = 2 - x. tentukanlah fungsi yang dinyatakan oleh f(x) + g²(x) + (f + g)(x) + (g - f)(x)
Jawab
g²(x) = (2 - x)²
= x² - 4x + 4
(f + g)(x) = (x + 1) + (2 - x)
= x + 1 + 2 - x
= 3
(g - f)(x) = (2 - x) - (x + 1)
= 2 - x - x - 1
= 1 - 2x
f(x) + g²(x) + (f + g)(x) + (g - f)(x) = (x + 1) + (x² - 4x + 4) + (3) + (1 - 2x)
= x² - 5x + 9
Soal Latihan Fungsi Komposisi 4.
Fungsi f : R → R dan g : R → R ditentukan oleh f(x) = 2x - 1 dan g(x) = x + 3. Tentukanlah:
a. (f ∘ g)(x) c. (f ∘ f)(x)
b. (g ∘ f)(x) d. (g ∘ g)(x)
Jawab
a. (f ∘ g)(x) = f(g(x))
= f(x + 3)
= 2(x + 3) - 1
= 2x + 6 - 1
= 2x + 5
b. (g ∘ f)(x) = g(f(x))
= g(2x - 1)
= (2x - 1) + 3
= 2x + 2
c. (f ∘ f)(x) = f(f(x))
= f(2x - 1)
= 2(2x - 1) - 1
= 4x - 2 - 1
= 4x - 3
d. (g ∘ g)(x) = g(g(x))
= g(x + 3)
= (x + 3) + 3
= x + 6
Soal Latihan Fungsi Komposisi 5.
Diketahui fungsi f(x) = 2x + 1 dan g(x) = x². Tentukanlah:
a. (f ∘ g)(x) c. (f ∘ f)(x)
b. (g ∘ f)(x) d. (g ∘ g)(x)
Jawab
a. (f ∘ g)(x) = f(g(x))
= f(x²)
= 2(x²) + 1
= 2x² + 1
b. (g ∘ f)(x) = g(f(x))
= g(2x + 1)
= (2x - 1)²
= 4x² - 4x + 1
c. (f ∘ f)(x) = f(f(x))
= f(2x + 1)
= 2(2x + 1) + 1
= 4x + 2 + 1
= 4x + 3
d. (g ∘ g)(x) = g(g(x))
= g(x²)
= (x²)²
= x⁴
Soal Latihan Fungsi Komposisi 6.
Diketahui g(x) = 2x + 3 dan (g ∘ f)(x) = 2x² + 4x + 5. Tentukanlah f(x).
Jawab
2x² + 4x + 5 = (g ∘ f)(x)
2x² + 4x + 5 = g(f(x))
2x² + 4x + 5 = 2(f(x)) + 3
2x² + 4x + 2 = 2(f(x))
x² + 2x + 1 = f(x)
f(x) = x² + 2x + 1
Soal Latihan Fungsi Komposisi 7.
Diketahui fungsi f : R → R dan g : R → R ditentukan oleh f(x) = 2x² dan g(x) = x - 3. Tentukanlah nilai x:
a. (f ∘ g)(x) = 2 c. (g ∘ f)(x) = 5
b. (f ∘ g)(x) = 4 d. (g ∘ f)(x) = -1
Jawab
a. 2 = (f ∘ g)(x)
2 = f(g(x))
2 = f(x - 3)
2 = 2(x - 3)²
1 = (x - 3)²
√1 = √(x - 3)²
1 = x - 3
x = 4
b. 4 = (f ∘ g)(x)
4 = f(g(x))
4 = f(x - 3)
4 = 2(x - 3)²
2 = (x - 3)²
√2 = √(x - 3)²
√2 = x - 3
x = √2 + 3
c. 5 = (g ∘ f)(x)
5 = g(f(x))
5 = g(2x²)
5 = (2x²) - 3
8 = 2x²
4 = x²
x = 2
d. -1 = (g ∘ f)(x)
-1 = g(f(x))
-1 = g(2x²)
-1 = (2x²) - 3
2 = 2x²
1 = x²
x = 1
Soal Latihan Fungsi Komposisi serta Pembahasannya - Demikianlah Soal Latihan Fungsi Komposisi serta Pembahasannya pada pertemuan kali ini, semoga pembahasan kali ini bisa bermanfaat ya bagi teman setia Sains Seru. Jika dalam pembahasan terdapat hal yang kurang jelas bisa di tanyakan di kolom komentar dibawah ya. Terimakasih sudah mau menyimak pembahasan kali ini sampai akhir, jangal lupa ya untuk selalu mengikuti update artikel disini ya. Salam SS. See You.